News Detail
复杂网络研究新方向:全齐性子网络
June 10, 2019
网络无标度特性,或者更广泛而言网络的异质性,一直是网络研究的热点——过去是研究热点,最近是争议热点:有人对无标度本身提出质疑,也有人否认它在现实网络中的普遍性。然而网络只有异质性应该被关注?异质性对网络结构和功能真的具有人们所认为的那么重要?人们激烈地争议着研究内容和结论,却忽视了对于研究视角的考察。或许这才是更重要的问题。越来越多的研究指出,在中观和介观尺度下,同质性的各种网络子结构,才是造成网络特性和功能差异的关键。
毫无疑问,网络具有度分布异质性,但这对于理解和研究网络远远不够。我们需要回过头来重新审视网络研究的视角,跳出桎梏,矫正视角,锋利工器,为网络研究开辟更广阔的新天地。
所谓复杂网络,即是将一个系统中的大量实体及它们之间的相互作用关系分别表示为节点和连边后所得到的网络表示。无论这个系统来自自然界还是人类社会,例如大量病历的分析处理、基因组测序、电力网络设计、交易数据分析和社交网络好友推荐等,都不用考虑这些实体间的交互关系在现实系统中表现出来的巨大差异,而从统一的视角对这些网络进行分析和研究。
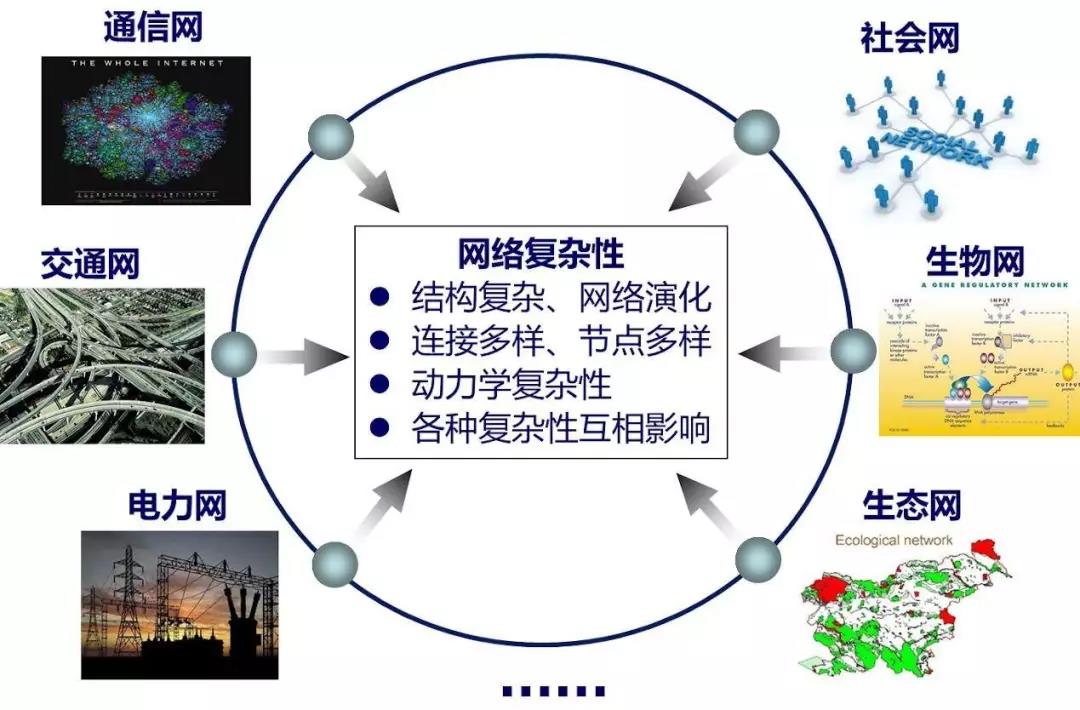
网络科学的理论及方法让我们能够更加深入地理解复杂系统的结构特征与演化机理,并对一些复杂系统中的传统问题提供超越原有认知范畴的解决方案。
复杂网络的独特之处在于它立足(大)数据,将跨越计算机科学、生物学、物理学、社会学、经济学以及电子商务等多学科的专业概念和研究问题整合起来,所以在面对新兴的交叉科学难题时具有先天优势。

网络是一种非常高效的对象化、结构化的数据存储结构。人脑是一个巨大的网络,万维网也同样构造成网状,这些都说明了网络是描述数据的一种极具灵活性的强大工具。网络科学能帮助人们设计更快、更有弹性的通信网络;能用于优化电力网络、电信网络和飞行航线等基础设施系统;可以为市场动态建模;能帮助理解生物系统中的同步;能用于分析人们之间的社会互动……
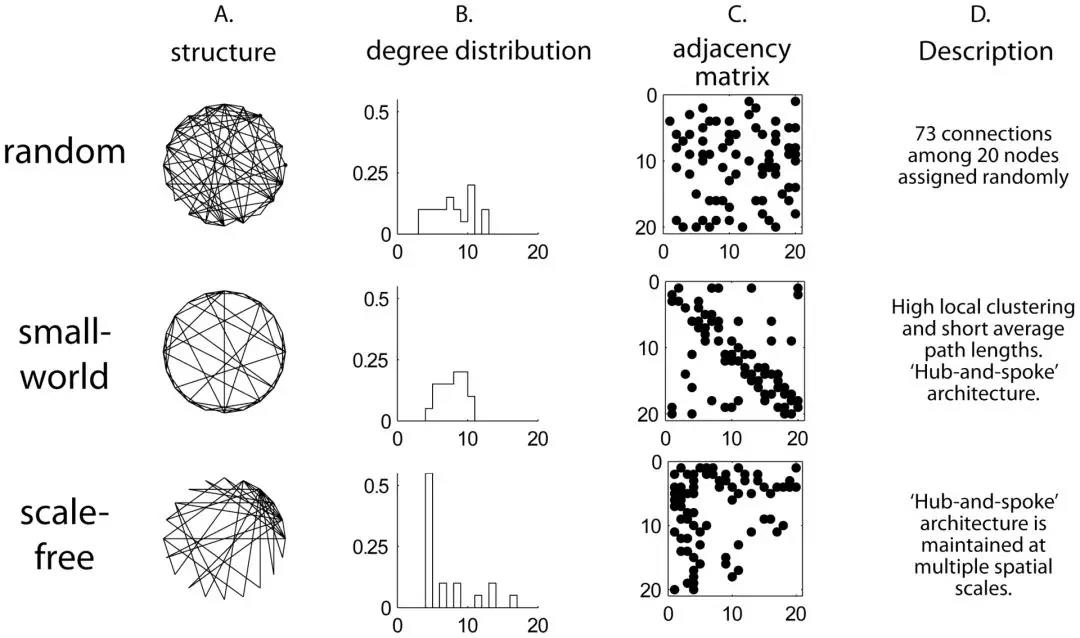
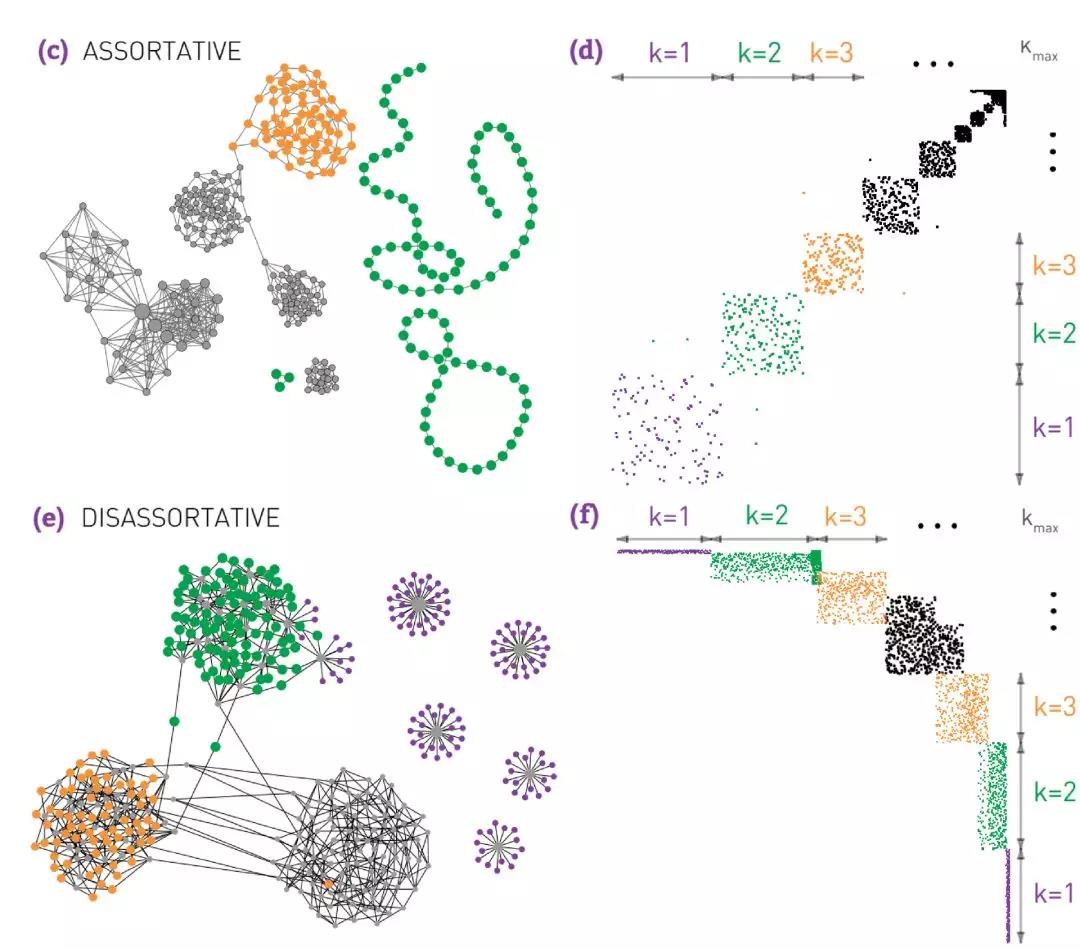
“异质性”从何而来?
当我们提及复杂网络的时候,必然绕不开节点和连边;当我们表示和计算网络的时候,必然绕不开邻接矩阵或邻接表。网络可以用邻接矩阵来描述,矩阵的阶数为网络中的节点数,节点的邻居数称为节点度。邻接矩阵的表示方法更容易使人们从节点及其邻居构成的邻域星结构的角度去研究网络,如无标度特性[5]。
所谓邻接,即直接相连。当我们研究矩阵和矩阵元素的时候,很多是在研究节点与邻居构成的邻域星型子结构,邻接表亦复如是。所以这种网络表示方式本身,赋予了我们一个“异质性”的视角——而这一点长久以来为人们所忽视。正因为我们一直是从本身具有“异质性偏见”的视角研究网络的,所以不难理解为什么长久以来异质性的度分布会获得广泛关注。但对事物的分析显然不能从单一角度进行,这样很容易产生片面甚至不正确的结论,有如一斑窥豹,所见仅为一斑[6]。
不可否认,以无标度特性为代表的网络异质性研究,在过去二十年中一直是网络研究的热点,也取得了丰硕成果。然而网络中只有异质性吗?答案显然是否定的,且近期对于无标度定义本身和相关结论争议四起[7-10]。导致这种争议产生的一个原因,就是因为越来越多的研究发现这种异质性的、低维度的视角对于更加深刻地认知网络复杂结构和行为还是远远不够的。
随着互联网技术发展及网络科学研究的深入,学者们发现基于星结构的传统认知模式已经不能满足现今各种网络和系统演化发展的现实及处理新近涌现出的科学问题,例如在线社交媒体上广泛存在的基于群组的“一对多”的信息传播模式、与人的高级认知功能相关的神经簇结构[11]、可控性网络子结构设计、局域物联网上的信息交换等等。
人们逐渐意识到网络的功能或各种动力学性质更多的与网络中的高阶拓扑结构、同质性子结构及网络的多个拓扑不变量等密切相关。由此转换现有的认知视角,探索并构建新的网络描述方法和研究框架,是为网络科学的当务之急。
受到庞加莱数学理念的启发,作者借鉴代数拓扑和拓扑图论的基本思想和工具提出了认知和描述网络的新视角——圈结构[12],注意到这里的圈不仅包含一般意义上的封闭环状连边结构,也包括全连通结构,构成封闭空间的洞结构(图5c)。将网络的认知视角从节点度转移到圈之后,就会发现普遍存在的、同质性的全齐性子网络。这里,全齐性网络定义为各个节点度相等、周长相等、路和相等的一类网络。
全齐性网络的典型例子如图5所示。其中c为最小2-洞,g为8节点近邻规则网络,h为10节点同步最优网络。
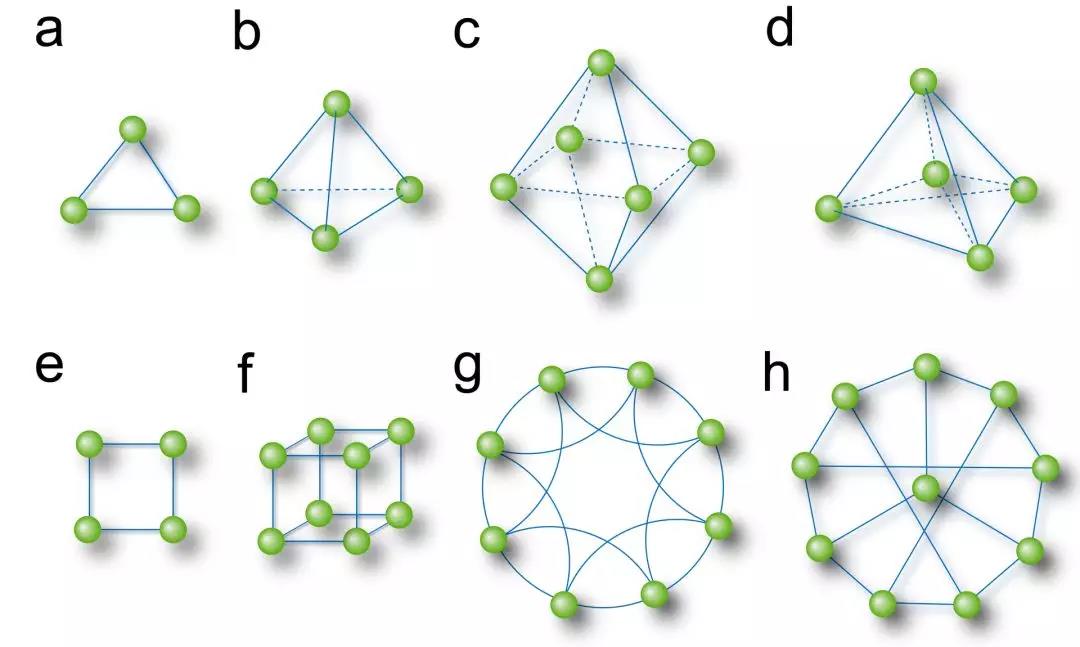
不同于微观尺度下的星结构,圈结构是一种中观或介观尺度下的网络结构,它超越了规模的限制,无论是三个节点构成的简单圈,还是300个节点构成的非冗余圈,亦或是基于封闭回路的更复杂圈结构,都被纳入这一视角。
早在十九世纪末,庞加莱发现边界是区分圆盘、球面、轮胎面等几何体的关键。他先把几何体剖分成称为单(纯)形的基本组成部分(点,线,三角形,四面体,…),从而引入了同调群、贝蒂数等多种工具并推导出欧拉-庞加莱公式,即单纯形的交错和等于贝蒂数的交错和。
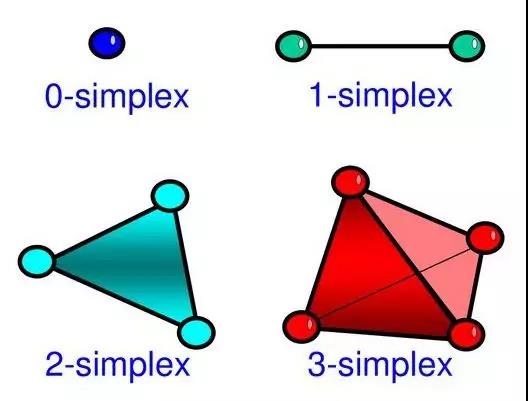
庞加莱的这一思想实质上是对复杂的拓扑几何体做“剖分”,进而化繁为简进行求解。受此启发,作者对复杂网络的结构进行类似的“剖分”,让庞加莱的数学理论顺理成章地应用于网络科学研究。之所以可以这样做,一个重要的原因是,网络中大量存在的全齐性结构(图论称为团,拓扑学称为单纯形),很多时候也是支持网络功能的重要基础结构。基于这些骨干单元,作者用一系列二元域上的向量空间来描述网络。
例如,以连线为基的向量空间C1,空间维数是连线数目;以三角形为基的向量空间C2,空间维数是三角形数目,等等。由于三角形的边是连线,它(C2)和以连线为基的向量空间(C1)作为两个相邻的向量空间可通过边界算子D2 : C2—>C1来建立关联,并用边界矩阵来表示和进行研究。
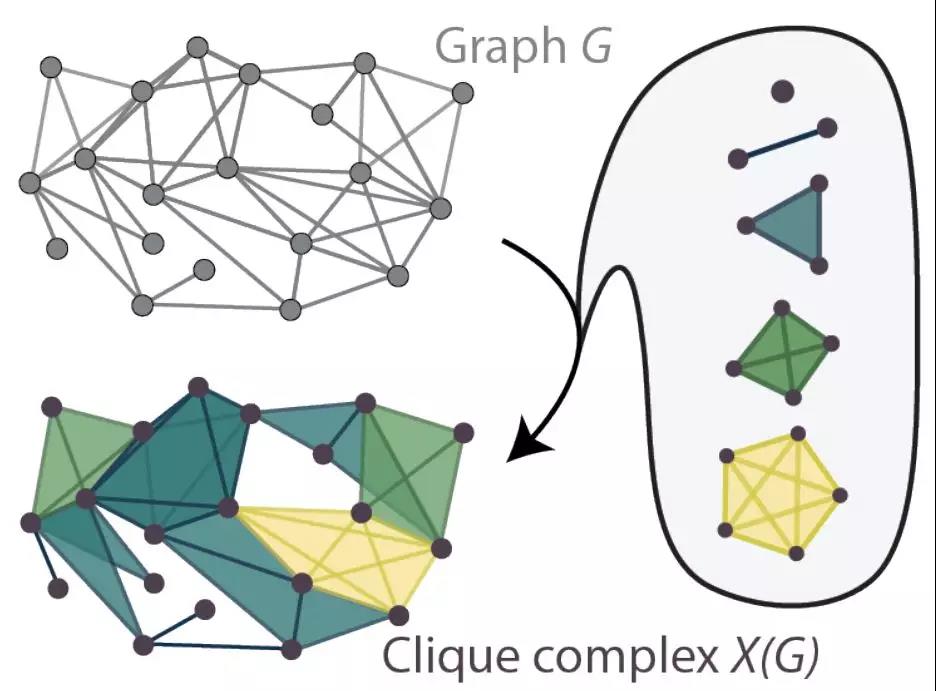
图7展示了使用单纯形将网络G(左上)剖分成复形(左下,由不同维度的单纯形构成)的过程。当然,这个复形可进一步按照边界算子分解为多个单纯形。
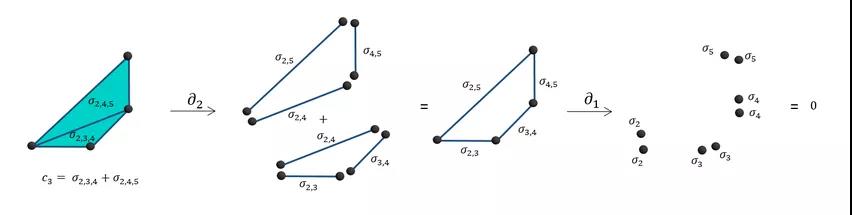
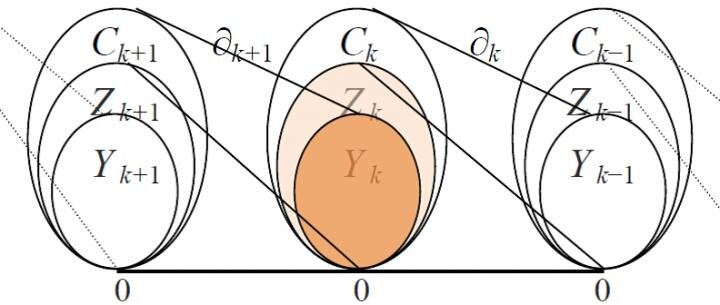
边界矩阵比邻接矩阵具有更丰富的数学含义和更多的可用工具。例如,通过边界矩阵的秩可计算网络重要不变量之一的贝蒂数,即网络无关k洞的数目,从而确定网络的同调群Zk/Yk。图9给出了边界算子和相关子空间的关系示意图。
笔者认为,以往的星结构主要是基于静态的结构去研究网络的,网络的演化要通过不同的矩阵表现出来;而圈结构将交互关系视为网络的本质,它立足于动态的功能对网络展开研究。在一定程度上,可以说圈就是交互本身,它依托于结构但不完全等价于结构。正如它所表示的交互关系,除了体现在直接连边上,还包括圈上的非直连节点间的交互。所以,星结构与圈结构在哲学上也值得深入研究。
代数拓扑的引入,是对现有网络研究模式的重要补充,也是对当前研究窘境的重大突破。作者们从新的认知视角——圈结构,依托于新的网络描述工具——(不同维单形构成的)向量空间,立足于现有的网络科学理论和方法并借鉴拓扑剖分的思想,将在全维度上对网络科学进行更深入的探索。
三、拓扑方法的广阔应用
实际上,这一趋势已经在多个领域崭露出来,如数据挖掘领域中拓扑数据分析(Topological Data Analysis,简称TDA)的兴起,机器学习中图网络(Graph Network)的提出,以及在数据库领域图形数据库的流行等,都清楚地显现出这个席卷各个领域的浪潮的来临。
拓扑学研究的是一些特殊的几何性质,这些性质在图形连续改变形状后还能继续保持不变,称为“拓扑性质”。而在复杂的高维数据内部也存在着类似的结构性质,我们可以形象地称之为数据的形状。
拓扑数据分析就是用拓扑学的理念方法对数据进行分析和信息挖掘。相比于主成分分析、聚类分析这些常用的方法,TDA不仅可以有效地捕捉高维数据空间的拓扑信息,还能够有效降低大规模数据处理的维度(而不丢失高维的信息)。
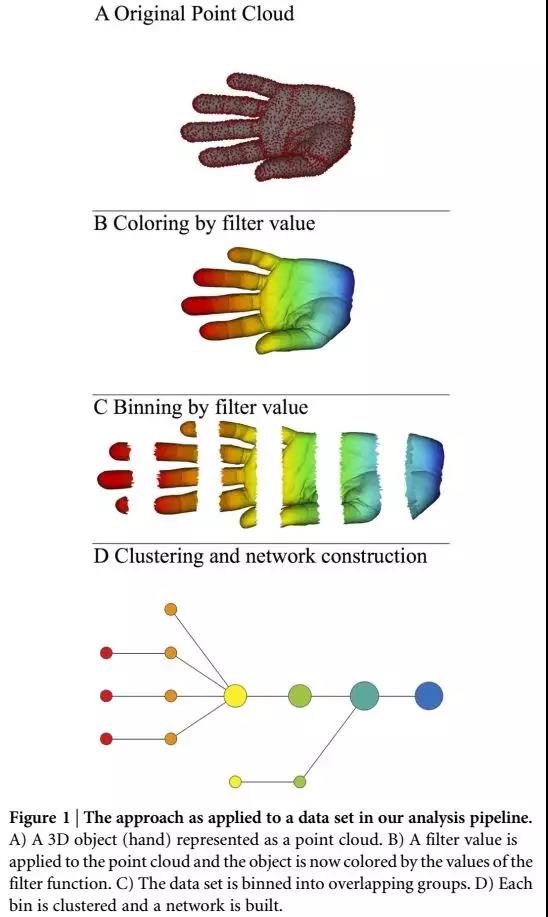
人们认为复杂数据中存在着内在固有的低维结构,由它们按照某种方式构成数据的高维形状。要理解数据的高维形状,就必须求助于拓扑分析。使用拓扑数据分析数据的过程,类似于拼图的过程——给你的只是拼图碎片,你要利用碎片间的关系拼出原来的完整图景。
目前这一方法已被用于基因表达数据分析,数据及图片的压缩感知,罕见病患者筛查以及解决评级缺失问题等。
作者们的探索最早源于2002年由汪小帆和陈关荣发现的网络同步准则[18]。那么,什么样的网络最容易同步呢?2013年,史定华,陈关荣和阎小勇等[19]通过优化引入了全齐性网络,发现周长越长、路和越短的全齐性网络在网络规模相同情况下同步能力最优。2016年,吕琳媛和周涛[20]等借助H算子建立了节点的度,H-指数和核数的内在联系,即网络的DHC定理。
在研究圈数指标的过程中,新近一项重要工作是Bassett研究组的Sizemore等人[11]于2018年发表的对大脑功能网络的实证研究,他们发现了网络中团和洞的特殊重要性。
2019年,范天龙,吕琳媛和史定华[12]提出圈结构的网络研究新视角,并对基于圈的指标进行了系统研究,提出刻画网络圈结构的圈数矩阵和衡量节点重要性的圈指标。
同年,史定华,吕琳媛和陈关荣[5]提出向量空间与边界算子,定义了网络中的拓扑运算与拓扑不变量。
一路走来,从源于物理的网络同步准则,经由优化导出了全齐性网络,其重要性得到大脑网络的实证检验,最终归结为代数拓扑的不变量指标。这一系列的成果本身就体现了物理、生物、数学等多学科交叉融合的意义和网络科学的价值,也预示着网络科学在代数拓扑的加持下,将重新焕发更耀眼的光彩。
参考文献
-
http://cgzh.seiee.sjtu.edu.cn/cgzh/minfo/2539_98.htm?n=1?n=1
-
http://www.lincoln.ac.nz/Research/Research/RC/CSBII/?sti=1
-
Michael S , Peterson J M , Borbala M , et al. Graph Theoretical Model of a Sensorimotor Connectome in Zebrafish[J]. PLoS ONE, 2012, 7(5):e37292-.
-
http://networksciencebook.com/chapter/7#impact-of-degree
-
Dinghua Shi, Linyuan Lü and Guanrong Chen, Totally homogeneous networks. Natl Sci Rev (April 2019) doi: 10.1093/nsr/nwz050.
-
https://baike.baidu.com/item/%E4%B8%80%E6%96%91%E7%AA%A5%E8%B1%B9/4700797?fr=aladdin
-
Shi D. Critical thinking of scale-free networks: similarities and differences in power-law random graphs[J]. National Science Review, 2014, 1(3): 337-338.
-
Broido A D, Clauset A. Scale-free networks are rare[J]. Nature communications, 2019, 10(1): 1017.
-
https://www.barabasilab.com/post/love-is-all-you-need
-
https://www.baidu.com/link?url=H90VhjEGHnoqQjFx0rFOW0AEOt9Ft2D3byWUq27rv37wrh0Y3rtcCjgFlDCg8exIKTpUYDpsoi34TfOUpk7b_TRtJ0MwL42dFJJ55G2T2iuiakaLezOLE-kiHfugrOlLTF_O3ccxQN82yP-zWXfU_K&wd=&eqid=9098e2de0027a595000000055cfb2f1f
-
Sizemore A, Giusti C, Kahn A, et al. Cliques and Cavities in the Human Connectome[J]. Journal of Computational Neuroscience, 2016, 44(1):115-145.
-
Fan T, Lü L, Shi D. Towards the cycle structures in complex network: A new perspective[J]. arXiv preprint arXiv:1903.01397, 2019.
-
Sizemore A E, Karuza E A, Giusti C, et al. Knowledge gaps in the early growth of semantic networks[J]. 2017.
-
Lum P Y, Singh G, Lehman A, et al. Extracting insights from the shape of complex data using topology[J]. Scientific Reports, 2013, 3:1236---.
-
Defferrard, Michaël, Bresson X, Vandergheynst P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering[J]. 2016.
-
https://en.wikipedia.org/wiki/Graph_database#/media/File:GraphDatabase_PropertyGraph.png
-
https://www.nextplatform.com/2018/09/19/the-graph-database-poised-to-pounce-on-the-mainstream/
-
Wang X F, Chen G. Synchronization in scale-free dynamical networks: robustness and fragility[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002, 49(1): 54-62.
-
Shi D, Chen G, Thong W W K, et al. Searching for optimal network topology with best possible synchronizability[J]. IEEE Circuits and Systems Magazine, 2013, 13(1): 66-75.
-
Lü L, Zhou T, Zhang Q M, et al. The H-index of a network node and its relation to degree and coreness[J]. Nature communications, 2016, 7: 10168.
