News Detail
Exploring deeper understanding and better description of networks
May 25, 2019
Exploring deeper understanding and better description of networks
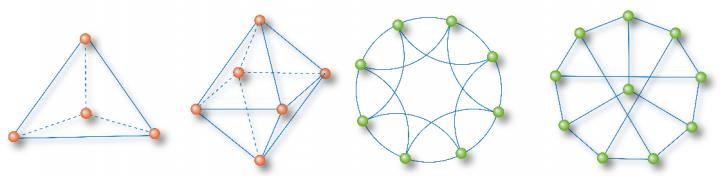
IMAGE: TOTALLY HOMOGENEOUS NETWORK EXAMPLES: A TETRAHEDRON, A MINIMAL 2-CAVITY NETWORK, AN 8-NODE NEAREST-NEIGHBOR NETWORK, AND A 10-NODE SYNCHRONIZATION-OPTIMAL NETWORK
Since the beginning of the last century, research on complex systems has made brilliant achievements, especially in the fields of chaos, fractals and networks. A network consists of nodes and edges, where nodes represent the elements of a complex system and edges describe the interactions among them. Such node-edge relations can be represented by an adjacency matrix, whose order equals the number of nodes and each row-sum corresponds to a node degree. The heterogeneity of node degrees leads to the emergence of star-shaped structures centered at hub nodes. To address the heterogeneity of node degrees, the scale-free network model came into play, attracting broad attention for quite a long time. To date, as the Internet technology further advances and the network research further develops, it has been realized that the traditional perception about star-based heterogeneous networks is insufficient to better describe the recently evolving complex networks and for deeper understanding of various newly arising network-scientific problems. For instance, there are many online communities in the Internet, depending on cycle-based social structures for group communication and information spreading. Network functioning and dynamical properties have more and closer connections with higher-order network topological features, homogeneous substructures and topological invariants. Thus, by shifting the focus from node degrees to cycle numbers, one could find many totally homogeneous subnetworks in complex networks. Here, a totally homogeneous network is defined to be a network with nodes having same degree, same girth (number of edges in the smallest cycle of a node), and same path-sum (sum of shortest paths to a node from all other nodes). A few typical examples are shown in Figure 1 for illustration.
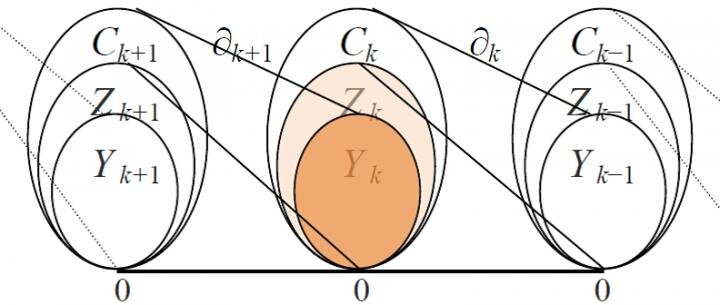
At the end of the 19th century, Poincaré found that boundaries are key in differentiating geometric shapes such as disks, spheres and tori. He decomposed a geometric object into basic components called simplexes (point, line, triangle, tetrahedron, etc.), and then introduced the concepts of homology group, Betti number and node-edge correlation matrix, and furthermore introduced the Euler-Poincaré formula, which shows that the alternative summation of simplexes equals the alternative summation of Betti numbers. The basic idea of Poincaré is to split a complex geometric shape, so as to simplify the procedure for a solution. He was able to do so because there are many totally homogeneous subnetworks, such as triangles and tetrahedrons (referred to as cliques in graph theory or simplexes in topology) in a complex network. They are basic structures for supporting network functions--differing from stars, they are cycles. With these basic elements, one could describe a network using a series of vector spaces over the binary field. For example, the vector space has edges as its basis, with dimension equal to the number of edges; the vector space has triangles as its basis, with dimension equal to the number of triangles, and so on. Since the boundary of a triangle consists of edges, the two adjacent vector spaces and can be correlated via a boundary operator , and its boundary matrix can be used for presentation and analysis. The boundary matrix has richer mathematical content and is more useful than the adjacency matrix. For instance, using the rank of the boundary matrix one can compute the Betti number, an important invariant of the network, which is the number of linearly independent cavities of different orders in the network, establishing a homology group. Figure 2 shows the relationships of some vector spaces and their corresponding boundary operators.
Our exploration started from 2002, when Xiaofan Wang and Guanrong Chen published the first criterion of network synchronization. It was followed by a series of works especially the introduction of totally homogenous networks via optimization by Dinghua Shi, Guanrong Chen and Xiaoyong Yan in 2013, revealing that the totally homogenous network with a longer girth and a shorter path-sum has a better synchronizability among networks of the same size. In addition, in 2006, Linyuan Lü and Tao Zhou used the H-operator to uncover the relationship among node degree, H-index and kernel value, establishing the DHC theorem. In the investigation of cycle index, an important work is the empirical study of Bassett et al. in 2018 on the brain functional network, where they pointed out the importance of cliques and cavities in network functioning. Last but not least, we recently discovered the close relationship of Euler characteristic numbers to the network synchronizability.
The aforementioned series of important progressive results, rooted from the physical criterion for network synchronization, to the totally homogeneous networks constructed via optimization, to the empirical verification of brain networks and to the invariant indexes in algebraic topology, demonstrates the significance and importance of interdisciplinary research in physics, biology and mathematics. Considering that this new direction of network structural analysis using algebraic topological tools is promising, we chose to publish our paper "Totally homogeneous networks" in National Science Review.
###
See the article:
Dinghua Shi, Linyuan Lü and Guanrong Chen,
Totally homogeneous networks
Natl Sci Rev (April 2019) doi: 10.1093/nsr/nwz050
https://doi.org/10.1093/nsr/nwz050
The National Science Review is the first comprehensive scholarly journal released in English in China that is aimed at linking the country's rapidly advancing community of scientists with the global frontiers of science and technology. The journal also aims to shine a worldwide spotlight on scientific research advances across China.
source:
1. eurekalert : Exploring deeper understanding and better description of networks
2. phys.org : Exploring deeper understanding and better description of networks
